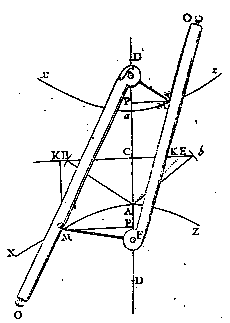
ピンと張った糸によって描く円錐曲線は、我々の研究室で作られ、“Traiteanalytique des sectionsconiques et de leur usage pour la resolution des equationsdans les problemes tant determinez q’indeterminez”と言ったDe l’Hospitalによって描かれた。ここで著者は、特にピンと張った糸を使った道具で、平面上に曲線として、放物線、楕円、双曲線を定義する。図では、道具が双曲線を描いているのがわかるであろう。  ２本の棒は、点Ｆと点Ｄで平面上を回転する。同じ長さlの2本の糸（l＞ＦＤかつ、棒の長さより短い）は棒の端と､平面上の回転軸とを繋ぐ。もし、その回転軸で２つの棒を回転させると同時に、糸をピンと張り、Ｍが棒に付いて運動しているならば、Ｍは双曲線を描く。実際、ＭＦの長さとＭＤの長さの差は一定で、棒の長さと糸の長さの差は等しい。

軌跡が双曲線になることの証明

数学実験室へ
いろいろな機構と数学実験トップへ
数学の歴史博物館