ちょうつがいのように組まれた平行四辺形を用いた円錐曲線の作図装置は、metric　geometryの見地をもとにした次の曲線の定義に関連性を有している。前記の曲線は、定点と定められた円周から等距離の平面上の点の軌跡である。2番目の図に示す放物線の作図装置は、F.Van Schooten　著の“DeOrganica conicarum sectionum In plano descriptione,tractatus.” で表された。

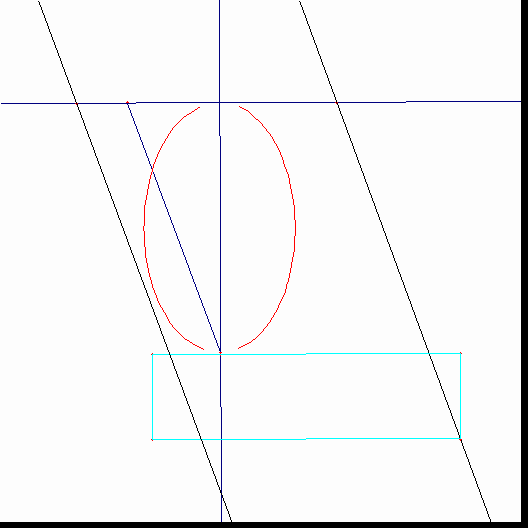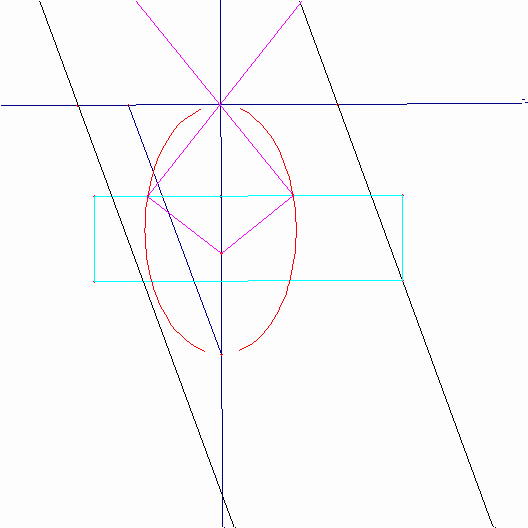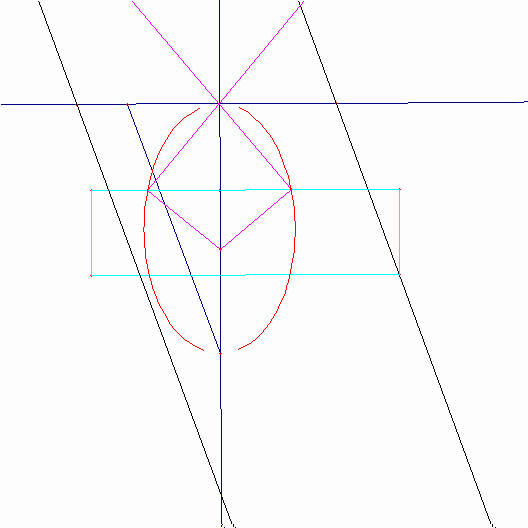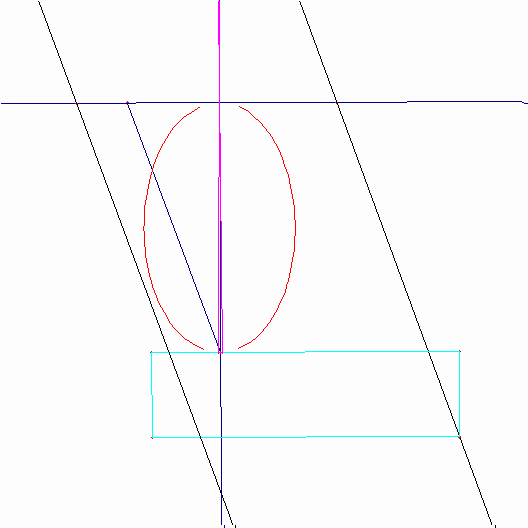
1番目の図は、楕円の作図を表している。その骨格は、点Pの周りを動いている棒（この棒は平面上にピンで固定されている）と、ちょうつがい化されたひし形ABCDから成り立っている。ひし形ABCDの頂点Aは回転の中心とされており、頂点Cは棒に連結されており、点Oからの距離がｌである。棒の上を動くピンが頂点Ｄであり、よってこの棒は、常にひし形の対角線を形成している。点Ｃが動くとき（点Ｃは点Ｏを中心とする半径ｌの円を描く）、ＯＣとＢＤの交点として定められている点Ｐは、焦点が点Ｏと点Ａである楕円を作図する。実は、ＰＯ＋ＰＡ＝ＰＯ＋ＰＣ＝ｌである。点Ｏを中心とする円は”directrix”と名づけられる。点Aが円の内部にある時、この作図装置は楕円を描き、点Aが円の外部にある時、双曲線が描かれる。もし、その円が直線であるならば、点Pによって描かれる曲線は点Aを焦点とする放物線を描く。