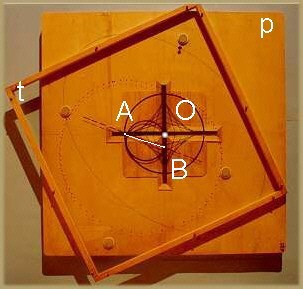
楕円を描く装置の中で、最も単純で、ひょっとすると最も古いものは、点ＡとＢを固定した棒で作られる。これらの点は2つの垂直な溝を動く2つのカーソルを回転する。棒の全ての点は、軸が溝である楕円を描く。溝の平面をｐ、線分ＡＢ上を動く平面をｔと名付ける。ｐ上のｔの動きを、固定された垂直な溝上の動きという。次のような事実がある：
１） Ｃを（平面ｔ上で）三角形ＯＡＢに外接する円、Ｄを点Ｏを中心とし、半径がＣの２倍である円とするならば、ｐ上のｔの動きはＤについてのＣの回転を得る。
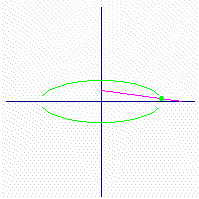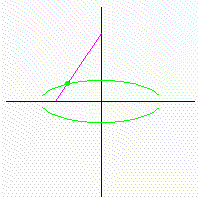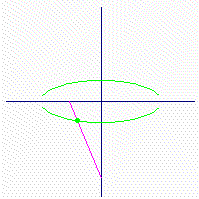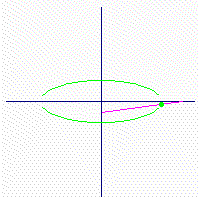
２） ｔ上のすべての点（Ｄの直径上を動く円Ｃの点を除く）は、楕円を描く。
３） Ｄのすべての直径は４つの尖点で、ipocycloidをつつむ。次に、直角になっていない２つの溝で道具を作った。ここでは、線分ＡＢのすべての点が楕円を描く：２つの共役直径は、溝上の線にある。

数学実験室へ
いろいろな機構と数学実験トップへ
数学の歴史博物館