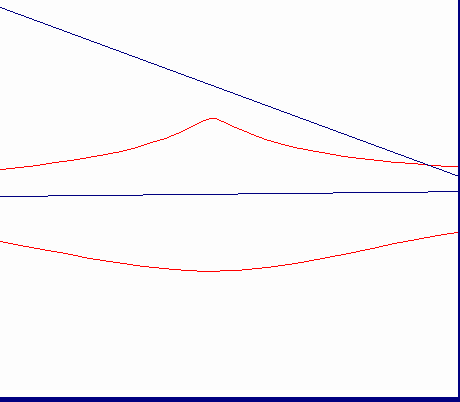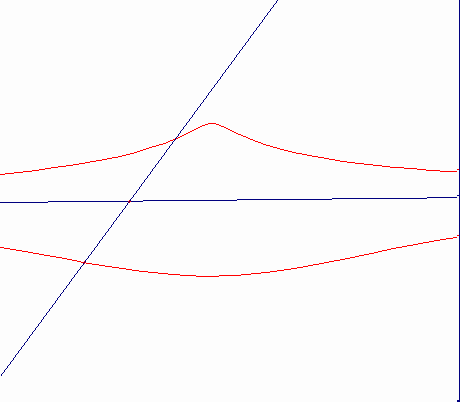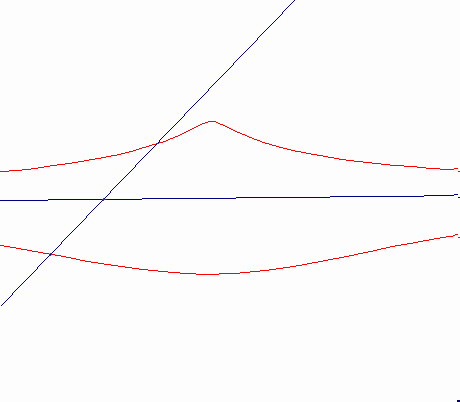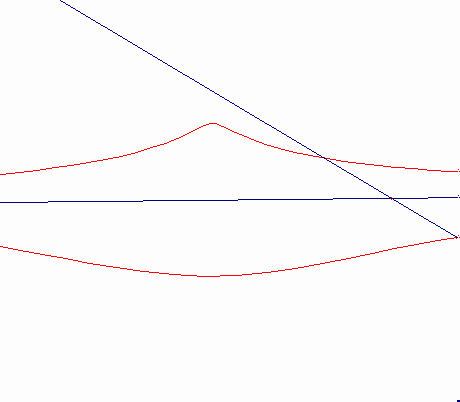
b>d
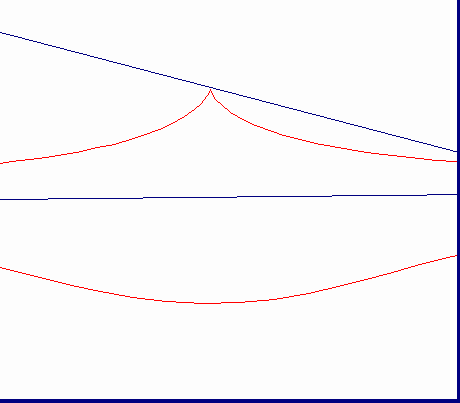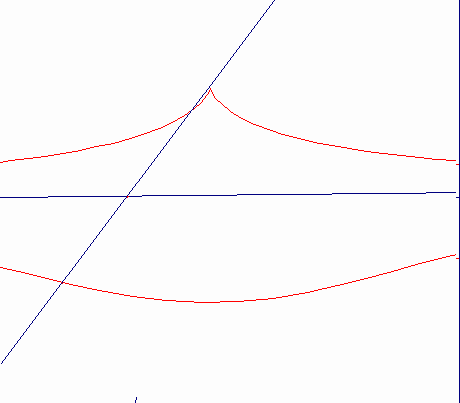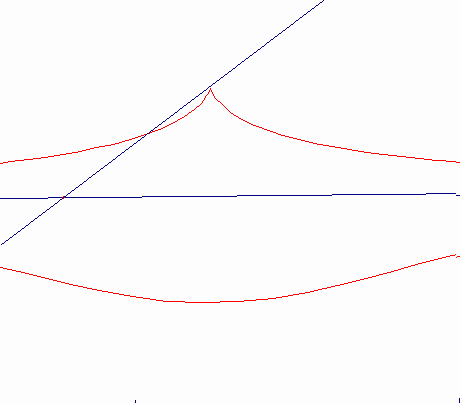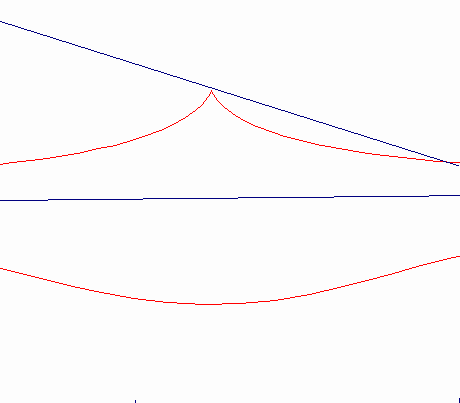
d>b b=d
曲線Bを基線として持つコンコイド
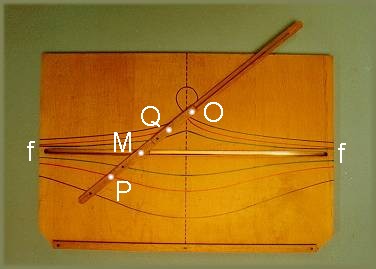
曲線B,点O,長さaの線分は,平面上に固定されている。点Oを通る全ての直線sは,点M,N,・・・・で,曲線Bと交わる。MP=MQ=a,NP=NQ=aの線分のついを直線s上にとる。直線sが点Oの回りを回転する時,点Pと点Qの軌跡は,基線B,極点O,距離aのコンコイドと呼ばれる。
ニコメデスのコンコイド(一般コンコイド曲線)のための
機械的リンケージ
−Mechanical linkage for the conchoid Nicomede−
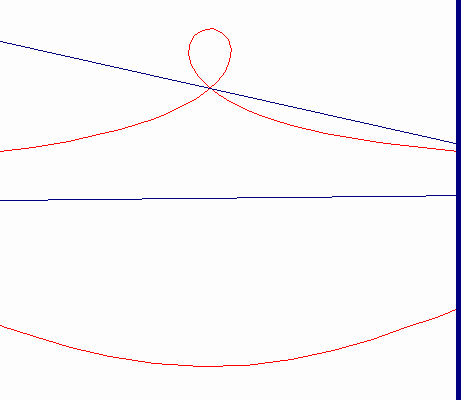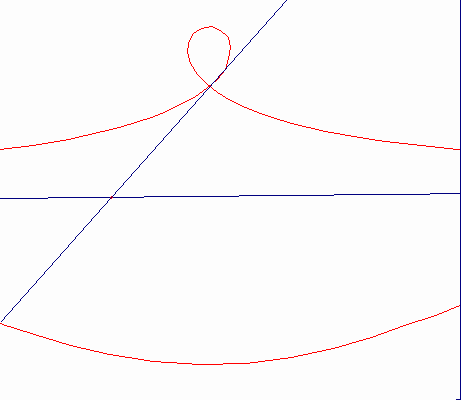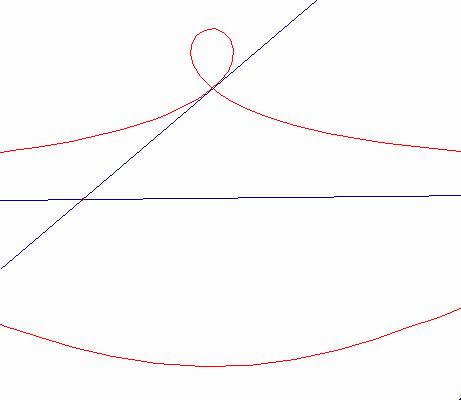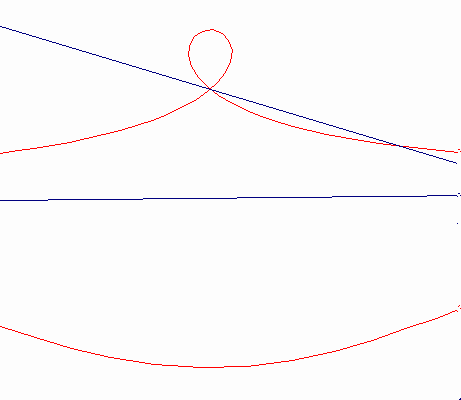
Nicomedeのコンコイドは,(曲線である)基線Bを直線として持っている。カーソルMは,ロットPQの1点で固定され,直線のみでff上を動く。ロットPQは,ffからの距離がdであり,平面上に固定されて点Oの回りを回転する。MP=MQ=bとなるようにロット上に2点P,Qをとる。点P,Qは極点O,基線ff,距離bを持つコンコイドを描く。コンコイドは,2つの流れを構成する。その1つは,b>dの時は尖点,b=dの時は結節点,d>bの時は孤立点を描く。コンコイドを正確にかくことができたり(コンパスは西暦200年頃のNicomedeの発明である)。また,立体を2倍したり,角を3等分する問題の解決の手助けになるので,この曲線はとても有名である。
b>d


d>b b=d


数学実験室へ
いろいろな機構と数学実験トップへ
数学の歴史博物館