Cissoido(シッソイド、疾走線)
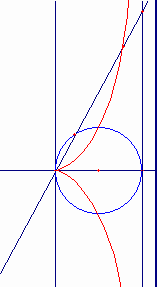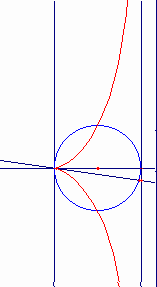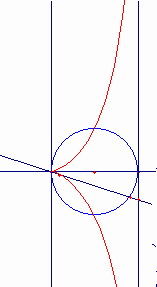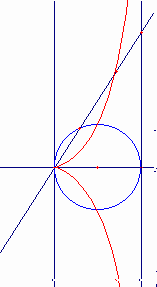
平面上にCDを直径とする円(シッソイドの基)を描く。 DTを円上の点Dにおける接線とする。点Cを通るすべての直線sはCと異なる点Eで円と交わり、点Fで直線DTと交わる。直線s上に点MをCM=EFとなるようにとる。このとき直線sを点Cの周りで回転させると、点Mは“シッソイド”と呼ばれる曲線を描く。

Strophoid(ストロフォイド)
直線AB、ACを描き、そのなす角BACを固定する。直線AB上に点Oを、Aに関しBの反対側にとる。線分OAの長さをストロフォイドの“パラメーター”と呼ぶ。rを点Oを通る直線とし、直線rと直線ACとの交点をNとする。直線r上に2点PとPをNに関し対称になるように、かつNP=NAとなるようにとる。このとき直線rを点Oの周りで回転させると、点Pは“ストロフォイド”と呼ばれる曲線を描く。
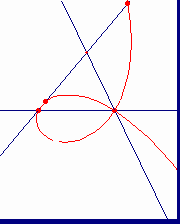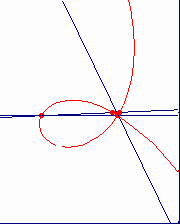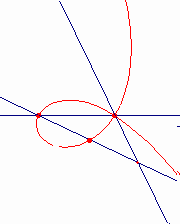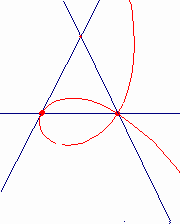
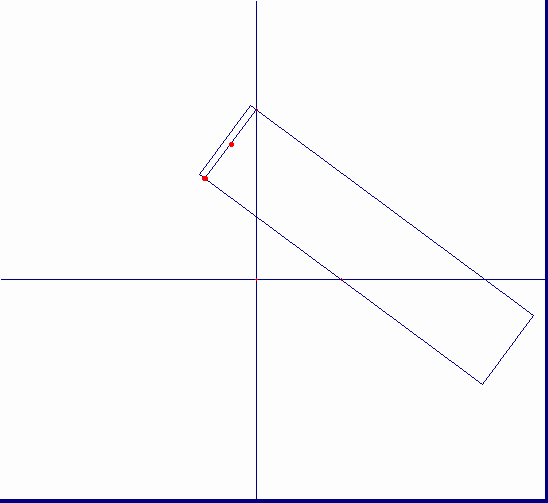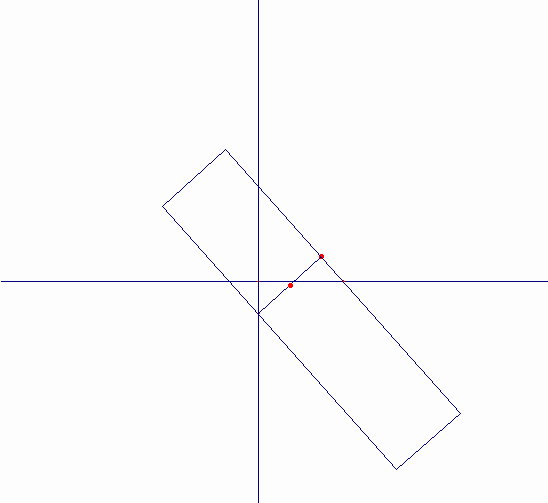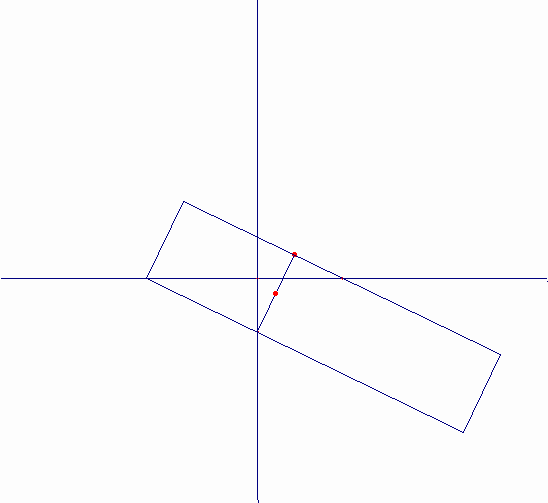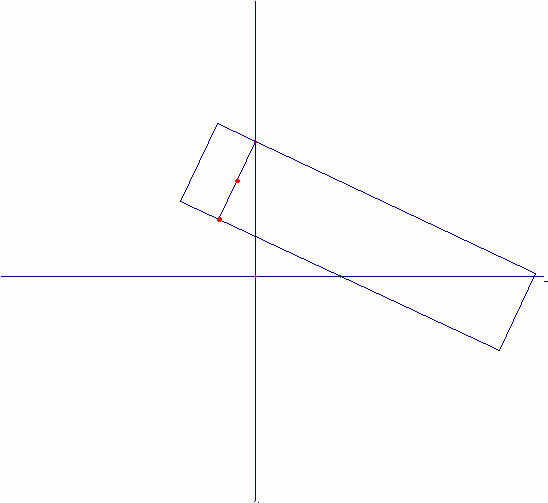
連続的な動きによる曲線の作り方は、ニュートン(“Arithmetica Universalis”1707)によっている。直角RKQは、次のように動く。頂点Qは溝ff上を動き、辺RKはピンHを軸としてその周りをHO=QK=CDとなるように回転する。QKの中点Mは、直径CD=2rの円を基とするシッソイドを描く。また、点Kは、ストロフォイドを描く。
数学実験室へ
いろいろな機構と数学実験トップへ
数学の歴史博物館