<一般的な定義><シッソイドの定義>
S、S’を任意の2つの曲線とし、Aを定点とする。Aを通る直線を引き、S及びS’との交点をそれぞれQ,Rとし、AP=QRとなるような点Pを決める。このとき、Pの軌跡は、Aに関するS及びS’のシッソイドと呼ばれる。
・Dioclesのシッソイド
Sを円周、Aを円周上の点、S'をAの正反対の円周上の点における接線とする。このときできるシッソイドを、ディオクレスのシッソイドという。
上の機構で描かれるのは,このDioclesのシッソイドである。
<ストロフォイドの定義>
Sを任意の曲線とし、Oを一つの点(極)、Aを他の点(定点)とする。Oを通る任意の直線とSとの交点をQとし、P’Q=QP=QAになるように点P,P’を直線上にとると、P及びP’の軌跡は、極O及び定点Aに関する、Sのストロフォイドと呼ばれる。
<証明>
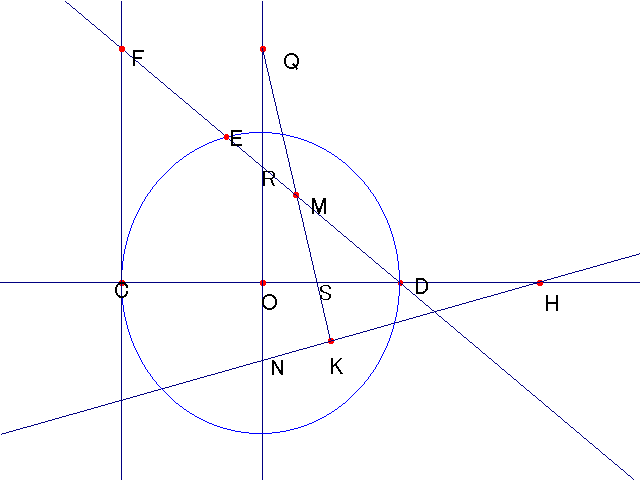
<点Mがシッソイドを描くことの証明>
点MはCD(ただし,CO=DO=HD)を直径とする円を基として,シッソイドを描く.
すなわち,FE=MDとなることを示せばよいが,そのためには,ER=MRを示せばよい.
三角形QOSと三角形HKSは合同で,また,仮定よりDO=MK.
よって,SD=SMとなり,三角形MSDは二等辺三角形.
従って,∠SMD=∠SDM.
また,三角形EODは,二等辺三角形なので,∠OED=∠ODE.
よって,∠OER=∠RMQ.
仮定よりEO=MQで,対頂角より∠ERO=∠MRQ.
従って,三角形EORと三角形MQRは合同であり,ER=MRが示せた.
<点Kがストロフォイドを描くことの証明>
NK=NOとなることを示せばよいが,
三角形QNKと三角形HNOが合同であることから明らか.
ニュートンの四角形に戻る
数学実験室へ
いろいろな機構と数学実験トップへ
数学の歴史博物館
お問い合わせ


