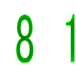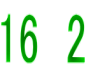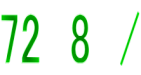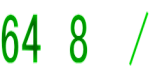（直径が９の円）　　 （一辺が９の正方形）

１　　　８セチャト　　/１　　　　　９セチャト

２　　１６セチャト　 　２　　　　１８セチャト

４　　３２セチャト　 　４　　　　３６セチャト

 /８　　６４セチャト 　 /８　　　　７２セチャト

（解説）リンドパピルス問題４１〜４３では、円柱の直径を与えて体積を出すように求めている。例えば、問題４１では、円柱の直径が９、高さが１０とされている。底面積を得るのに、直径からその１／９を引き、残りを２乗して円の面積を６４としている。円の面積と直径との関係について、どのようにして発見したかについてアーメスは説明していない。しかし、体積を求める問題が面積どうしの関係を述べている問題４８の前にあるということから、何らかの過程を経て体積を求め、そこから円の面積を求める方法を得ていたと考えるのが自然である。直径が９の底面を持つ円柱と同じ高さで様々な底面を持つ正四角柱を作り、円柱に満たした水が、底面が１辺８の正四角柱をほとんど一杯に満たすことを知った。つまり、正四角柱の底面の１辺が円柱の直径からその１／９を引くことで決定されると判断したと考えられる。