�ڐ��̊I��}�Ɋւ�����Ǝ��H
�\�A�|���j�E�X�̉~���Ȑ��_��p���ā\
�}�g��w��w�@�C�m�ے����猤���ȁ@�@�����@�r�N
�P�D�͂��߂�
�u���w�͎Љ�ł͖��ɗ����Ȃ��v�ƍl���A���w�ɑ���ӗ~��ړI�������Ă��鐶�k���������������B���̂悤�ȏ͐��w�w�K�ɂ�����u���w�̊�{�I�ȊT�O�⌴���E�@���̗����v��u���w�I�v�l�̈琬�v�Ƃ������w����̖ړI�̈���B������Ă��Ȃ����Ƃ̌���ł͂Ȃ����ƍl������B�u�����E�S�v���Ȃ�����w�K�ӗ~�������A�u�T�O�⌴���E�@���̗����v��u���w�I�v�l�̈琬�v�͒B������ɂ����A�w�K���e���蒅�����w�Ԉӗ~�ɂȂ���Ȃ��Ƃ������z�����̂悤�ȏ݂����Ă���B
�@�����P�T�N�x������{�����u�V�w�K�w���v�́v�ɂ́A�u���w�ɂ�����T�O�̌`���⌴���E�@���̔F���̉ߒ��Ɛl�Ԃ╶���̊ւ��𒆐S�Ƃ��āA���w�j�I�Șb������グ��v���ƂŁA�u���ʂ�}�`�ɂ��Ă̊T�O�����l�Ԃ̊����ɂ�������Ĕ��W���Ă������Ƃ𗝉����A���w�ɑ��鋻���E�S�����߂�B�v�Ƃ����L�q��������B���̓��e����A�u���w�j�v�̖����Ƃ��āA�u���w�Ɛl�Ԃ̊ւ��v��`���u�����E�S�v�����߂Ă������Ƃ��ł���Ƃ������Ƃ���������B���ꂪ�A�u���w��b�v�̖ڕW�ɂ���u���w�I�Ȍ�����l�����̗ǂ���F�������w�����p����ԓx����Ă�B�v���Ƃ�B���\�ɂ���̂ł͂Ȃ����B�E�c����(2001)�́u���w�j�́A���w��l�̉c�݂Ƃ��Ď��o����Ӗ��ł̐��w�̕����I����̊o���_�@�������B�v�Əq�ׁA�u���w�j���T���߂ɂ�萶�k���w�Ԑ��w�̕����I����̊o���@������B�v�Ƃ��Ă���B
�@��s�����ɂ́A�A�|���j�E�X�́u�~���Ȑ��_�v�����������̂Ƃ��āA�㓡�i1997�j�A��t���i1998�j������A�A�|���j�E�X�́u�ڐG�v�̌��T�������A�J�u����p�������ފJ�����������̂Ƃ��č����i2001�j�����邪�A�A�|���j�E�X�́u�~���Ȑ��_�v�̌��T�������A�J�u����p�������ފJ����������s�����͖������������Ă��Ȃ��B
�@�����ŁA�~���Ȑ��̋N���ɏœ_�����āA�~���Ȑ��i��ɕ������j�Ƃ��̐ڐ��̊I��}�ɂ��ĒǑ̌������A���̐��ʂɂ��čl�@����B
�Q�D�����ړI�E�������@
�����ړI�F���w�j�����ƂɎ�����邱�Ƃɂ��A���k���w��ł������w��l�̉c�݂Ƃ��đ����A���w�ς̕ϗe�������炵�A���w�ɑ��鋻���E�S�����߂Ă������Ƃ��ł��邩���l�@����B
�ړI�B���̂��߁A�ȉ����ۑ�Ƃ���B
�ۑ�P�F���w�j�����ƂɎ�����邱�Ƃɂ��A���w�W�I�ɑ����A���w�ɑ��錩����ς��A�����E�S�����߂Ă������Ƃ��ł��邩�B
�ۑ�Q�F��}���l���邱�Ƃɂ��A�~���Ȑ��₻�̐ڐ����I�ɑ����A������[�߂邱�Ƃ��ł��邩�B
�������@�F���T��p�������j�I���ނ��J�����A�����p�������Ǝ��H���s���B���Ƃ̎��O�E����ɐ��w�Ɋւ���ӎ���₤�A���P�[�g�A�e���Ƃ��ƂɎ��Ƃɑ��銴�z��₤�A���P�[�g�y�ю��Ƃ��B�e�����r�f�I�����Ƃɍl�@����B
�R�D���ƓW�J
�{�����ł͌��T�Ƃ��ăA�|���j�E�X�́w�~���Ȑ��_�x�A�w���[�N���b�h���_�x���ނƂ��ėp�����B�~���Ȑ��̍�}���@�₻�̐ڐ��̍�}���@���l���A��}�c�[��(Cabri Geometry �U)��p���č�}���A���k���w��ł����~���Ȑ��Ɣ�r����B
�P���ԖځF�������̒�`�𗝉����A��ᒆ���̍�}�ƕ�������̓_�̍�}���l����
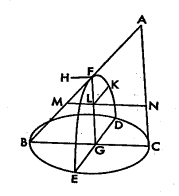 �@���O�ۑ�ɁA�~��������̐ڐ��ɂ��āA�ڐ��̕����������߂���ƁA�ڐ�����}��������ۂ����B�������̂悤�ȉ~���Ȑ��ɂ��čl�����Ă����M���V�A���w�́u���[�N���b�h���_�v�U������14�����グ��B�l���̊�{�Ɂu���̍l���v�E�u�ʐς̂��Ă͂߁v���g���Ă��邱�Ƃ𗝉����邽�߂ɁA��ᒆ���̊W�̏ؖ����l���A���[�N���b�h���_�̏ؖ��Ɣ�r����B
�@���O�ۑ�ɁA�~��������̐ڐ��ɂ��āA�ڐ��̕����������߂���ƁA�ڐ�����}��������ۂ����B�������̂悤�ȉ~���Ȑ��ɂ��čl�����Ă����M���V�A���w�́u���[�N���b�h���_�v�U������14�����グ��B�l���̊�{�Ɂu���̍l���v�E�u�ʐς̂��Ă͂߁v���g���Ă��邱�Ƃ𗝉����邽�߂ɁA��ᒆ���̊W�̏ؖ����l���A���[�N���b�h���_�̏ؖ��Ɣ�r����B
���ɁA�A�|���j�E�X���A�~���Ȑ��ɂ��Ă̓����̍l�����u�Ή~�����قȂ�ؒf���@�Őؒf���ĂR��ނ̋Ȑ������v�Ƃ������Ƃ�m��B
�~���Ȑ��_�̖���11(�������̒�`)�̏ؖ��𗝉�����B
���T���߂ɂ��ẮA�M���V�A��E���e�����E�p���E���{�����e�L�X�g�Ɍf�ڂ��A���e�̗����͓��{����p�����B
 �Q���ԖځF��}�c�[���ɂ��������̒�`��p���ĕ������̍�}������
�Q���ԖځF��}�c�[���ɂ��������̒�`��p���ĕ������̍�}������
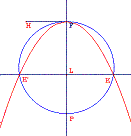
��ᒆ���̊W�iRS�Q��PS�ESQ�j�����藧�_�q��PS�ASQ�����}�ł��邱�Ƃ𗘗p���āA�������̒�`�iKL�Q��FH�EFL�j�����_K�̍�}���@���l����B�J�u���W�I���g���[�U���g���č�}���A�O�Ղ��������ɂȂ邱�Ƃ��m�F����B
 �R���ԖځF�������̐ڐ��̐����𗝉����A�ڐ�����}����B���ɑo�Ȑ��E�ȉ~�̒�`�Ɛڐ��̐����𗝉�����B
�R���ԖځF�������̐ڐ��̐����𗝉����A�ڐ�����}����B���ɑo�Ȑ��E�ȉ~�̒�`�Ɛڐ��̐����𗝉�����B
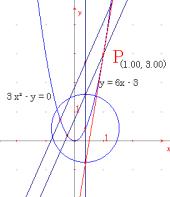
�@�ڐ��̐����Őڐ��E���a�E�c�������̊W���l���A��������̓_�ɂ�����ڐ���������O�̓_����̐ڐ��̍�}���@���l���A�J�u����p���č�}����B���O�ɋ��߂��ڐ��̕������ƈ�v���邱�Ƃ��m�F����B
�@���ɁA����12�i�o�Ȑ��̒�`�j�Ɩ���13�i�ȉ~�̒�`�j�ɂ��Ă��������Ɠ��l�ɂ��Ē�`�Ɛڐ��̍�}���@�𗝉�����B��}���ꂽ�o�Ȑ��̐ڐ����A�J�u���̋@�\�𗘗p���đo�Ȑ���ȉ~�ɕό`���Ă��������ۂ���A�ȉ~�̐ڐ��ɂȂ邱�Ƃ�̌�����B
�S�D���ʁE�l�@
�ۑ�P�́u���w�j�����ƂɎ�����邱�Ƃɂ��A���w�W�I�ɑ����A���w�ɑ��錩����ς��A�����E�S�����߂Ă������Ƃ��ł��邩�B�v�ɂ��āA���ƌ�̃A���P�[�g���A�P���ڂ́A�����������w�K���Ă������w�Ɣ�ׂ�Əؖ��̒����⏑�����A�p���̋L�q�Ɍ˘f���A��a�����o�������k�̔����������������A�R���ڂɂȂ�Ɠ��e�𗝉����ăM���V�A���w�Ɗw�K���Ă������w�̈Ⴂ�₻�̂��炵����F�߂銴�z�ɂȂ��Ă���B����܂Ŏ����������w��ł����}�`���A�I���O�̌Ñ�M���V�A����ɗ��̐}�`�̐ؒf�ʂƂ����`�ŏڂ��������ɋL�q����A�������A���������g��Ȃ��\�����@�ŏ�����Ă��������̐��w�����߂��銈����ʂ��āA���k�͂���܂Ŋw��ł������w�Ɣ�Ⴂ�������A�l�̉c�݂Ƃ��Ă̐��w�𑨂��Ȃ���������[�߁A�����E�S�����߂Ă���B
�ȏォ��A���w�j�����ƂɎ�����邱�Ƃɂ��A���w�W�I�ɑ����A���w�ɑ��錩����ς��A�����E�S�����߂Ă������Ƃ��ł����ƌ�����B
�ۑ�Q�́u��}���l���邱�Ƃɂ��A�~���Ȑ��₻�̐ڐ����I�ɑ����A������[�߂邱�Ƃ��ł��邩�B�v�ɂ��� �A���ƌ�̃A���P�[�g����A�}�����邱�Ƃ������������A��}�ɂ��}�`�̐����̗��������[�߂邱�Ƃ��ł��邱�Ƃ�������A�}���}�̑���������Ă���B�܂��A�J�u���i��}�c�[���j���g�����Ƃ����߂Ăł������̂ŁA���߂͋@�\�ɑ��ċ����������Ă������A�ŏI�I�ɂ͂��̗L������������Ɏ����Ă���B����̊��z�ɂ́A���O�̃A���P�[�g�ɂȂ������}�`�ƕ������̊W�ɂ��Ă̋L�q�������A��}���邱�Ƃō�}���@�������邾���łȂ��A�㐔���S�Ɋw��ł������w�ɑ��A�I���_�̏d�v�����ĔF�����A�Ƒ㐔�̌��т������߁A�}�`�ɑ��闝�����[�܂��Ă��邱�Ƃ�������B
�T�D������
�@�{�����ł́A���T�����ނɎ����ꂽ���w�j�̊w�K���A���k�̐��w�ς̕ϗe�ɍv���ł��A���w�ɑ��鋻���E�S�����߂邱�Ƃ��ł��邩�ɏœ_�ĂĂ����B�A�|���j�E�X�̉~���Ȑ��_���ނɁA��`�ɂ��~���Ȑ��Ƃ��̐ڐ��̍�}�ɂ��āA�������𒆐S�ɍ�}���@���l���A��}�c�[����p���Ċw�K���邱�ƂŁA���w�W�I�ɑ����A���w�ɑ���u�����E�S�v�����߂邱�Ƃ��ł��邱�Ƃ����������B
�@���ƌ�̃A���P�[�g�ɂ����āA���w�ɑ��ė������[�܂苻���E�S�����܂����l�q�����k�Ɍ��ꂽ�Ƃ����_�ŁA���̎��H���ʂ����������͑傫���ƍl������B�V�w�K�w���v�̂̂��Ƃł��̂悤�Ȉӎ��k�Ɏ�������w�K�͉\�ł��邪�A���w�j�����p�����w�K����萔�w�ς̕ϗe�ɍv���ł���Ƃ�����B
������Ƃ������k�́A��}�c�[���i�J�u���j���g���̂����߂Ăł��������ƁA����ɂȂ��̂Ɏ��Ԃ��\���ɂƂ�Ȃ��������Ƃ���A�����̒��ɂ͍�}���}�`�̗��������������Ƃ��}���@�������ł������ƈȊO�ɍ�}�c�[���̋@�\�ɑ�����̂�����ꂽ�B���z�ɂ́A��}���@�𗝉����邽�߂ɂ̓R���s���[�^�����łȂ��A��ɂ���}���@���l�������Ƃŗ������[�܂�l�q������ꂽ�B
����A���w�j�������ꂽ���ފJ���ƁA�R���s���[�^�̌��ʓI�Ȋ��p���@�ɂ��Ă̌����ۑ�Ƃ��Ď��g��ł��������B
�Q�l����
�y1�zR�DCatesby�@Taliaferro�i1939�j�DON�@CONIC�@SECTIONS�@BY�@APOLLONIUS�@OF�@PERGA�D GREAT�@BOOKS�@OF�@THE�@WESTERN�@WORLD�i1952�j�DUniversity�@of�@Chicago�DENCYCLOPEDIA�@BRITANNICA�CINC�Dpp.595�|804
�y2�z�E�c����(2001)�D�ٕ����̌�����݂����w�̕����I����̊o���Ɋւ����l�@�\�B�ꂽ�����Ƃ��Ă̐��w�ς̈ӎ����ƕϗe�����߂ā\�D�}�g���w���猤���@��20���Dpp.39�|48
�y3�z�E�c����(1987)�D���w�w�K�ɂ����鐔�w�j�̗��p�Ɋւ����l�@�D�}�g��w������ꒆ�E�����w�Z�����A��26�W�Dpp.159�|174
�y4�z�����p��(2001)�D���Z���w�ɂ����鐔�w�j�̓����Ɋւ����l�@�`�A�|���j�E�X�̖��̉�@��ʂ��ā`�D���E�̋���ے����v�̓����Ɨ��j�����u���̐��w����\�㐔�E�E����For All�v���W�F�N�g�̐V�W�J�\�D���w�Z�E�����w�Z���w�ȋ���ے��J���Ɋւ��錤���i�W�j�D�}�g��w���w����w�������Dpp.143�|160