アポロニウスの命題について(BOOK1 命題52-58)
ここで、アポロニウスは放物線、楕円、双曲線の意味について、面積作図を
用いて説明しています。全体を大まかに説明すると、以下のようになります。
まず、ある平面に直線を2本ひきます。この二本の直線は、直角に交わるか
もしくはそうでないかで場合わけします。ある一定の作図方法により,もとの直線
どうしの比が,そこで描かれる図形の面積の比で表されることを示しています。
またそれだけでなく、円錐曲線の意味についても説明しています。
ここで使われているモデルが楕円であるため、これから先は楕円について
のみの説明とします。
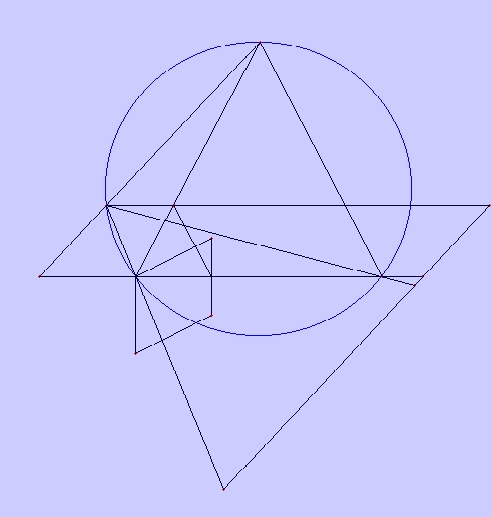
下のように作図するのですが、その過程を示します。ここでは,最初に与え
られる二本の直線を直角と仮定しています。まず、弧ABに対して,長い方の
弧を描き,その中点をDとします。DAとDBを結び、AXをAX=ACとなるようにし、
Xを通って、XOをDBに平行にひき、Oを通って、OFをABに平行にひき、DFを結
び、ABを延長した交点をEとする。そしてAFとFBを結んで延長し、FA上に適当
にとられた点をGとし、Gを通ってGLをDEに平行にひきABの延長の交点をKと
する。またFOを延長してそれとGKの交点をLとする。ここまでの一連の作図は,
同一平面Z上で行われたものとする。
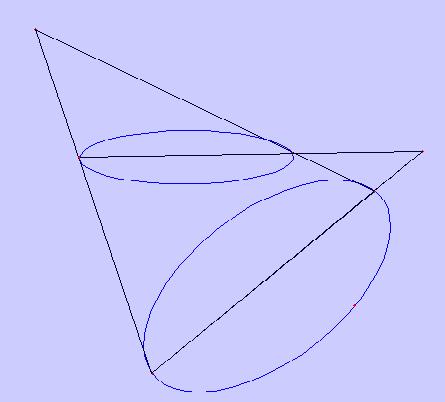
ここで,GHを直径に持つ円を描き、それを円GHNとします。ただしこの円は,
三角形HGFと垂直であるとする。(つまり、もとにあった平面Zとは垂直になる)
この円を底面とし頂点をFと考えると、この円錐は直円錐となる。EKを含み,Zに
垂直な平面で円錐を切ったときにあらわれる図形がABを長軸に持つ楕円である。
ここで少し計算してみよう
まず、
DE: EF = DE×EF : EF 2
ところが、
BE×EA: EF2 =( BE : EF )×( AE : EF )
そして、
AE: EF = AK : KG = FL : LG
これより、
BA: AC = ( FL : LG )×( FL : LH )
これはつまり、
FL2= GL×LH
ゆえに、
BA : AC = FL2 : ( GL×LH )
これが成り立つときはいつでもは,図の通径となる

数学実験室へ
いろいろな機構と数学実験トップへ
数学の歴史博物館
お問い合わせ
