 丂丂仮俙俢俛佭仮俠俛俢
丂丂仮俙俢俛佭仮俠俛俢儀儖僰乕僀偺嶌恾偑恀偵Lemniscate偱偁傞偐傪帵偡丏懄偪婡夿揑偵掕媊偝傟偨嬋慄乮Lemniscate乯傪戙悢揑偵夝庍偡傞丏乮掕媊偵娭偟偰偼埲壓偺峫嶡傪尒傛丏
 丂丂仮俙俢俛佭仮俠俛俢
丂丂仮俙俢俛佭仮俠俛俢
丂丂丂佹俙俢亖俠俛丆俙俛亖俠俢丆俛俢嫟捠丗嶰曈憡摍
丂丂丂傛傝佢俙俛俢亖佢俠俢俛丂乧嘆
丂丂摨條偵丂仮俙俢俠佭仮俠俛俙丂
丂丂傛傝佢俢俠俙亖佢俛俙俠丂乧嘇
丂丂嘆嘇傛傝丂擇妏憡摍偱仮俶俙俠佷仮俶俛俢
丂丂亪俙俠//俛俢
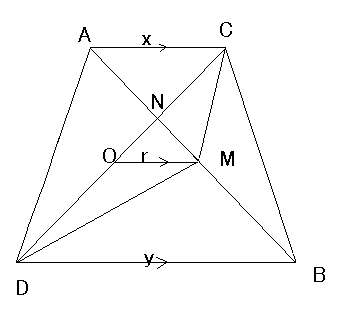
揰俷丆俵偑俠俢丆俙俛偺拞揰偱偁傞偙偲偵拲堄偟丆摨條偵偟偰
丂丂亪俙俠//俷俵
丂丂偙偙偱丆俷俵亖倰丆俙俠亖倶丆俢俛亖倷丆佢俶俷俵亖兤偲偍偔丏
丂丂捈慄俷俵偲俙俢偲俠俛偺岎揰傪峫偊傞丏拞揰楢寢掕棟傛傝丆
丂丂丂倷乛俀亄倷乛俀亅倰亖倶乛俀亄倶乛俀亄倰
丂丂丂俀倰亖倷亅倶
丂丂丂亪倰俀亖乮倷亅倶乯俀乛係丂乧嘊
丂丂堦曽丆梋尫掕棟傛傝丆俀們俀亖倷俀亄係們俀亅係們倷cos兤
俀們俀亖倶俀亄係們俀亅係們倶cos乮兾亅兤乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂 亖倶俀亄係們俀亄係們倶cos兤丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂傛傝倸俀亅係們cos兤倸亄俀們俀亖侽偺俀夝偑倶丆倷乮倶亙倷乯偱偁傞偐傜丆
丂丂夝偲學悢偺娭學偐傜丆丂倶亄倷亖係們cos兤
丂丂丂丂丂丂丂丂丂丂丂丂丂倶倷亖俀們俀
丂丂丂丂丂丂丂丂亖乮侾俇們俀丂cos俀兤亅俉們俀乯乛係
丂丂丂丂丂丂丂丂亖係們俀乮乮cos俀兤亄侾乯乛俀乯亅俀們俀
丂丂丂丂丂丂丂丂亖俀們俀cos俀兤
丂亪倰俀亖俀們俀cos俀兤丂丂丂丂丂丂仭丂丂
侾丏俁庬椶偺掕媊
丂丂Lemniscate偺掕媊偵偮偄偰懡妏揑偵峫嶡偡傞丏戞堦偵丆杮暥偵偁傞Lemniscate偺掕媊偼梫栺偡傞偲丆
乽敿宎倰偺墌俠偲墌奜偺揰俷傪屌掕偡傞丏掕揰俷傪捠傞捈慄倱偲墌俠偲偺岎揰傪俵丆俶偲偟丆捈慄倱忋偵俷俹亖俷俻亖俵俶傪枮偨偡揰俹丆俻傪偲傞丏捈慄倱傪掕揰俷偺廃傝傪夞偡偙偲偱弌棃傞揰俹丆俻偺婳愓傪Lemniscate偲傛傇乿
偱偁傞丏偙傟偼僐儞僐僀僪偺掕媊偵偍偄偰嬋慄俛傪墌俠偲偟丆婎揰俷傪墌俠奜偵偲傞摿庩側応崌偲偟偰偱偁傞偙偲偑暘偐傞丏偙偙偱嬶懱揑側嶌恾朄傪尦偵掕媊偝傟偰偄傞偙偲偵拲栚偡傞丏偮傑傝堦掕偺忦審傪梌偊偨婡夿偑峔惉偝傟偰偄偰丆偁傞晹暘傪摦偐偡偙偲偵傛偭偰昤偔揰偺婳愓傪嬋慄偲偟偰掕媊偝傟偰偄傞偺偱偁傞丏偙偺傛偆側掕媊傪婡夿揑掕媊偲屇傇偙偲偵偡傞丏僄僕僾僩丒僶價儘僯傾悢妛媦傃屆戙僊儕僔儍婜乮婭尦慜俁侽侽擭埲慜乯偵偍偄偰偼丆悢妛偼應抧妛傗揤暥妛側偳幚惗妶偵偦偭偨傕偺偱偁傝丆婡夿乮摴嬶乯偵傛偭偰懳徾傪應傝丆昤偔乮嶌恾偡傞乯偙偲偑悢妛偺傂偲偮偺僥乕儅偱偁偭偨丏偦偙偵偼乽憂堄乿偲乽峔惉乿丆乽榑徹乿偺俁抜奒偑撪曪偝傟偰偄傞丏偙偙偱廳帇偝傟傞傋偒崁栚偼乽憂堄乿乽峔惉乿偱偁傠偆丏応崌偵墳偠偰婡夿傪憂傞偙偲偼堦庬偺捈姶乮傂傜傔偒乯偲愊傒廳偹傜傟偨宱尡偵埶懚偟傛偆丏
丂偙偙偵婡夿妛偺栤戣偺傂偲偮偱偁傞堦抳惈乮well-defined乯偺栤戣偑尒偰偲傟傛偆丏偮傑傝偁傞嬋慄乮墲乆偵偟偰恾宍偲屇偽傟傞乯偵懳偟丆婡夿乮偵傛傞嶌恾乯偼堦堄偵掕傑傜側偄丏偙傟偱偼摨偠嬋慄偵懳偟條乆側掕媊偑懚嵼偟丆傑偨嶌恾偝傟偨嬋慄偑媮傔傞嬋慄偐偳偆偐敾暿乮暘椶乯偡傞偙偲偑崲擄偱偁傞丏偙偺堦抳惈偺栤戣傪夵慞偡傞偙偲丆尵偄姺偊傞偲乽榑徹乿傪廳帇偡傞偙偲偑媮傔傜傟傞丏偙偺傛偆側娤揰偵棫偭偨掕媊偑婔壗揑掕媊偱偁傞丏偙偙偵Lemniscate偺婔壗妛揑掕媊偼丆
乽暯柺忋偱俀掕揰俥丆俥乫偐傜偺嫍棧偺愊偑俹俥丒俹俥乫亖乮俥俥乫乛俀乯俀偲側傞傛偆側揰俹偺婳愓乮廤崌乯傪Lemniscate偲傛傇乿
偱偁傞丏栜榑偺偙偲丆婡夿揑掕媊偵傛偭偰掕傔傜傟偨嬋慄偲婔壗妛揑偵掕傔傜傟偰嬋慄偑堎側傞傛偆偱偼堄枴偑柍偄丏儐乕僋儕僢僪乮Euclid乯婜偵偍偄偰丆悢妛幰偼嬋慄傪暯柺忋偺堦掕忦審壓偺揰偺廤崌偲偟偰峫偊偨丏偦偺攚宨偵偼婔壗妛偺棽惙偲榑徹庡媊偑偁傞丏懄偪丆幚嵺婡夿揑偵嶌恾偝傟偨嬋慄偲偄偆嬶懱揑懳徾偐傜扙媝偟丆岞棟宯偺拞偱拪徾揑偵嬋慄傪埖偆偙偲偵傛傝婔壗偲弶摍戙悢偺棟榑傪梡偄偰懳徾傪峫嶡乮榑徹乯偡傞偙偲偑壜擻偵側偭偨偲尵偊傛偆丏
丂師偵偙偺嬋慄偵嵗昗傪擖傟傞偙偲偱丆娭悢乮曽掱幃乯偲偟偰埖偆掕媊偑偁傞丏偙傟傪戙悢揑乮夝愅揑乯掕媊偲屇傇丏Lemniscate偺応崌丆
乽倶倷捈岎嵗昗昞帵乮倶俀亄倷俀乯俀亅俀們俀乮倶俀亅倷俀乯丆嬌嵗昗昞帵倰俀亖俀們俀們倧倱乮俀兤乯乿
偲側傞丏偙偺掕媊偺棙揰偼丆嬶懱揑乮帇妎揑乯偵嬋慄偑尒偊偰偙側偔偰傕戙悢傗夝愅揑庤朄偵傛傝幃憖嶌傪偡傞偙偲偱嬋慄偺惈幙偑暘偐傞偙偲偩傠偆丏
俀丏奺乆偺掕媊偺摿怓
丂婡夿揑掕媊偼嬋慄傪幚嵺偵摼傞偙偲偑偱偒傞揰偱桪傟偰偄傞丏傑偨僷儔儊乕僞乮忦審乯傪曄偊傞偙偲偑梕堈偱丆偦偺偙偲偱堎側傞嬋慄傪摼傞偙偲偑偱偒傞丏偨偩偟忋弎偺傛偆偵堦偮偺嬋慄偵懳偟偰丆峔惉忋堎側傞婡夿偑婔偮傕懚嵼偡傞偙偲丆懄偪掕媊偑婔偮偐懚嵼偡傞壜擻惈偑偁傞丏偩偐傜婡夿偵傛偭偰昤偐傟偨嬋慄偑媮傔傞嬋慄側偺偐偳偆偐乮堦抳惈乯傪榑徹偡傞偺偑崲擄偱偁傞偲偄偆揰偱掕媊偵濨枂偝傪姶偠傞丏偙偺堦抳惈傪崕暈偟偨婔壗揑掕媊偼丆嬋慄偺幚懱傪梊憐偡傞偙偲偑壜擻偱妿偮柸枾偵嬋慄傪榑徹偡傞偙偲偑偱偒傞丏崱擔墲乆偵偟偰幚嵺偵惓妋側嬋慄傪昤偔昁梫惈偼彮側偄丏偩偐傜掕媊偲偟偰偙偺婔壗揑掕媊偑埖傢傟傞偙偲偑懡偄偺偱偁傞丏戙悢揑掕媊偵偍偄偰偼丆嵟憗嬋慄偺幚憸傪憐憸偡傞偙偲偼崲擄側偙偲偱偁傞丏偟偐偟嬶懱惈傪婞媝偡傞偙偲偱摼傜傟偨拪徾榑偼丆屄乆偺嬋慄偲偄偆榞傪墇偊偰廳梫偱偁傞丏偦偙偱偼懡乆丆曄姺傗旝愊暘偲偄偭偨庤朄偑梡偄傜傟丆傛傝崅埵偺奣擮傊偲堏峴偡傞丏偙偺揰偱婔壗揑掕媊傪戙悢揑偵撉傒捈偡嶌嬈偼懡暘偵尒傜傟傞丏偟偐偟掕媊偺忦審傪彮偟曄壔偝偣偨偙偲偵傛偭偰偱偒傞嬋慄偵偮偄偰峫嶡偡傞偙偲偑擄偟偄丏乮偙偙偱偄偆曄壔偵傛傞悇堏偼楢懕惈傗旝暘壜擻惈偲偄偭偨夝愅揑曄壔偱偼側偄丏乯
俁丏娭楢惈
掕媊偺曄慗偐傜尒偰傕丆嬋慄傪婡夿揑掕媊偐傜婔壗揑掕媊丆戙悢揑掕媊偵夝庍偟偰偄偔偙偲偼梕堈偱偁傞丏偦偙偵偼懡乆徹柧傪梫偡傞偑丆尵偄姺偊傟偽徹柧偡傞偩偗偱夝庍偱偒傞偺偱偁傞丏堦曽丆偙偺媡偼崲擄傪嬌傔傞丏偦傟偼婡夿揑掕媊偵偟偰傕婔壗揑掕媊偵偟偰傕掕媊偺拞偵乽憂堄乿偑娷傑傟偰偄傞偐傜偱偁傞丏偮傑傝戙悢揑偵掕媊偝傟偨嬋慄傪幚嵺偵昤偔嵺丆傑偨曽掱幃偺僷儔儊乕僞傪偳偺傛偆偵憖嶌偡傟偽椶帡偺嬋慄傪摼傞偙偲偑弌棃傞偺偐側偳偺忬嫷傪峫偊傟偽偦偺夝庍偺曄姺偺崲擄偝偑暘偐傠偆丏
偙偙偱師偺傛偆側帠幚偑偁傞丏婔壗揑掕媊傗戙悢揑掕媊偵傛傝嬋慄傪巜摫偡傞偙偲偼丆帪偵嬋慄偺幚憸傪尒偢偵忋妸傝偺棟夝偵宷偑傞壜擻惈偑偁傞丏摿偵丆掕媊偲嬋慄偺娭楢惈偑婓敄偱偁傞偨傔丆掕媊娫偺憡屳惈偮傑傝嬋慄娫偺憡屳惈偑柍偔側傞嫲傟偑偁傞丏偙傟偼婔壗揑掕媊傗戙悢揑掕媊偺寚揰傪擛幚偵昞偟偰偄傞丏掕媊傪曄偊傞偙偲偲嬋慄偺曄壔偲偺娫偺屳姺惈傪攟偆昁梫惈偑偁傞丏偦偺偨傔偵偼嬋慄傪幚嵺昤偔昁梫偑偁傞偩傠偆丏偮傑傝嬋慄傪婡夿揑偵夝庍偡傞偙偲偑桳梡偱偁傞偲峫偊傞丏偟偐偟愭弎偺傛偆偵戙悢揑掕媊偵傛傞嬋慄傪婡夿揑掕媊偲偟偰夝庍偡傞偙偲偼崲擄偱偁偭偨丏偙偙偵嶐崱偺嬋慄巜摫偺尷奅傪姶偠傞丏傂偲偮偺庤抜偲偟偰僥僋僲儘僕乕偺棙梡偑偆偐偑偊傞丏椺偊偽偙偺儂乕儉儁乕僕傕慠傝偱偁傝丆傑偨乽僇僽儕乿傗乽俧俠乿偲偄偭偨婔壗僜僼僩偺棙梡傕慠傝偱偁傠偆丏
悢妛幚尡幒傊
偄傠偄傠側婡峔偲悢妛幚尡僩僢僾傊
悢妛偺楌巎攷暔娰